Algorithm of $\alpha$ constrained Powell's method

In Powell's method, we repeat linear search toward conjugate directions and search the minimum value of $f(\mbox{\boldmath$x$})$. In linear search methods, we search the minimum value one-dimensionally along the direction vector $\mbox{\boldmath$d$}$ from a certain point $\mbox{\boldmath$x$}$. In other words, we regard $f(\mbox{\boldmath$x$}+a\mbox{\boldmath$d$})$ as the function of $a$ and search the minimum value of it. Hereafter, $Powell_\alpha$ represents the algorithm of $\alpha$ constrained Powell's method and Linear-search$_\alpha$ represents linear search method which compares search points by $\alpha$ level comparisons. $Powell_\alpha$ is described in C like language as follows:

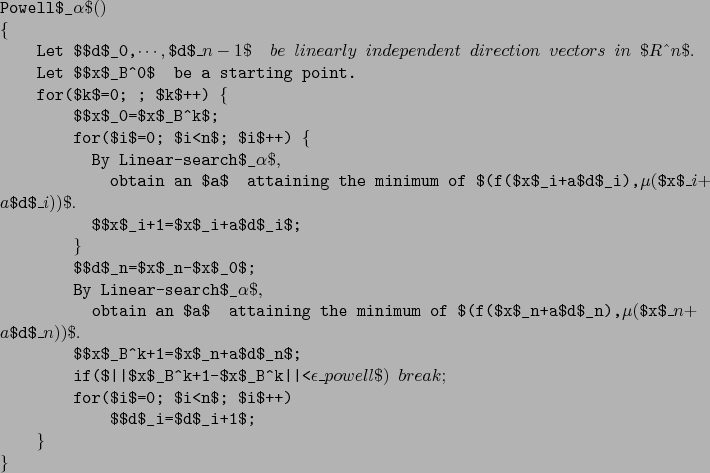
where $\epsilon_{powell}$ is accuracy of the search. We may select the $n$ unit vectors indicating the direction of each axis of $R^n$ as $n$ initial direction vectors.

We realize Linear-search$_\alpha$ by the combination of bracketing$_\alpha$ and golden$_\alpha$. Bracketing$_\alpha$ and golden$_\alpha$ represent algorithms of bracketing method and golden cut method which use $\alpha$ level comparisons as order relations, respectively. The algorithms are described in C like language as follows:

where $F_1=(3-\sqrt{5})/2$, $F_2=(\sqrt{5}-1)/2$. $\epsilon_{golden}$ is accuracy of the search.